What Are Non Adjacent Angles

7.1.3: Nonadjacent Angles

Last updated
Salve every bit PDF

Page ID: 38725

Lesson

Allow'southward look at angles that are not correct next to one another.

Do \(\PageIndex{1}\): Finding Related Statements

Given \(a\) and \(b\) are numbers, and \(a+b=180\), which statements also must be true?

\(a=180-b\qquad a-180=b\qquad 360=2a+2b\qquad a=90\text{ and }b=90\)

Exercise \(\PageIndex{2}\): Polygon Angles

Use any useful tools in the geometry toolkit to identify whatsoever pairs of angles in these figures that are complementary or supplementary.

Do \(\PageIndex{three}\): Vertical Angles

Employ a straightedge to depict two intersecting lines. Utilize a protractor to measure all iv angles whose vertex is located at the intersection.

Compare your cartoon and measurements to the people in your group. Make a conjecture about the relationships between angle measures at an intersection.

Exercise \(\PageIndex{iv}\): Row Game: Angles

Find the measure of the angles in one cavalcade. Your partner will work on the other column. Cheque in with your partner after you finish each row. Your answers in each row should be the same. If your answers aren't the same, piece of work together to find the mistake and correct it.

cavalcade A

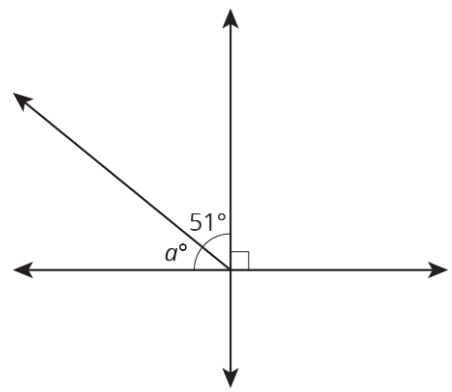
\(P\) is on line \(grand\). Observe the value of \(a\).

Find the value of \(a\).

column B

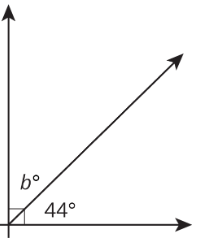
Detect the value of \(b\).

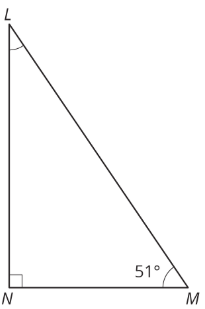
In correct triangle \(LMN\), angles \(L\) and \(M\) are complementary. Find the measure out of angle \(L\).

column A

Angle \(C\) and angle \(E\) are supplementary. Find the measure of angle \(Due east\).

Find the value of \(c\).

Two angles are complementary. I angle measures 37 degrees. Find the measure out of the other angle.

column B

\(X\) is on line \(WY\). Find the value of \(b\).

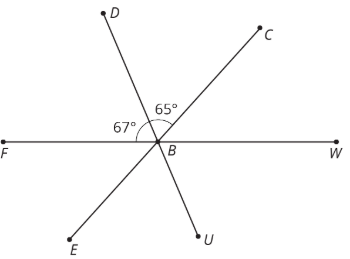
\(B\) is on line \(FW\). Find the mensurate of bending \(CBW\).

Two angles are supplementary. One angle measures 127 degrees. Detect the measure of the other bending.

Summary

When ii lines cross, they form two pairs of vertical angles. Vertical angles are across the intersection indicate from each other.

Vertical angles always take equal measure. Nosotros tin see this because they are always supplementary with the same angle. For example:

This is always true!

\(a+b=180\) so \(a=180-b\).

\(c+b=180\) so \(c=180-b\).

That means \(a=c\).

Glossary Entries

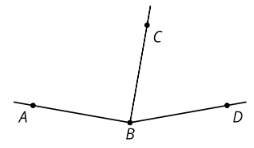
Definition: Adjacent Angles

Adjacent angles share a side and a vertex.

In this diagram, angle \(ABC\) is adjacent to angle \(DBC\).

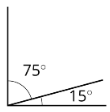
Definition: Complementary

Complementary angles have measures that add up to xc degrees.

For instance, a \(xv^{\circ}\) angle and a \(75^{\circ}\) bending are complementary.

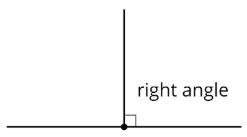
Definition: Right Angle

A right angle is half of a direct bending. It measures 90 degrees.

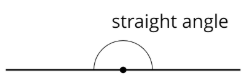
Definition: Straight Angle

A straight angle is an angle that forms a straight line. It measures 180 degrees.

Definition: Supplementary

Supplementary angles have measures that add upwards to 180 degrees.

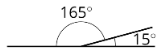
For example, a \(fifteen^{\circ}\) angle and a \(165^{\circ}\) angle are supplementary.

Definition: Vertical Angles

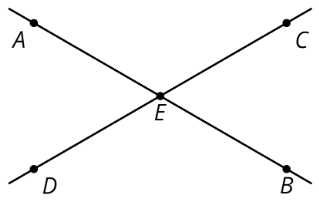
Vertical angles are opposite angles that share the same vertex. They are formed by a pair of intersecting lines. Their bending measures are equal.

For case, angles \(AEC\) and \(DEB\) are vertical angles. If bending \(AEC\) measures \(120^{\circ}\), and then angle \(DEB\) must as well measure \(120^{\circ}\).

Angles \(AED\) and \(BEC\) are another pair of vertical angles.

Practice

Exercise \(\PageIndex{5}\)

Two lines intersect. Find the value of \(b\) and \(c\).

Practice \(\PageIndex{six}\)

In this effigy, angles \(R\) and \(S\) are complementary. Find the measure of angle \(S\).

Practice \(\PageIndex{seven}\)

If 2 angles are both vertical and supplementary, can we decide the angles? Is it possible to exist both vertical and complementary? If so, can you lot determine the angles? Explain how yous know.

Practice \(\PageIndex{8}\)

Match each expression in the first list with an equivalent expression from the 2nd list.

\(5(ten+1)-2x+11\)
\(2x+2+x+five\)
\(\frac{-3}{8}10-9+\frac{5}{8}x+1\)
\(ii.06x-five.53+4.98-9.02\)
\(99x+44\)

\(\frac{1}{4}x-viii\)
\(\frac{1}{two}(6x+14)\)
\(11(9x+4)\)
\(3x+16\)
\(2.06x+(-five.53)+iv.98+(-9.02)\)

(From Unit 6.4.5)

Exercise \(\PageIndex{nine}\)

Gene each expression.

\(15a-13a\)
\(-6x-18y\)
\(36abc+54ad\)

(From Unit 6.4.ii)

Exercise \(\PageIndex{x}\)

The directors of a dance show await many students to participate but don't notwithstanding know how many students volition come. The directors need seven students to work on the technical crew. The remainder of the students work on dance routines in groups of 9. For the show to work, they demand at least six total groups working on dance routines.

Write and solve an inequality to correspond this situation, and graph the solution on a number line.
Write a sentence to the directors well-nigh the number of students they need.

(From Unit of measurement 6.3.5)

Exercise \(\PageIndex{11}\)

A minor dog gets fed \(\frac{three}{4}\) cup of dog food twice a solar day. Using \(d\) for the number of days and \(f\) for the amount of nutrient in cups, write an equation relating the variables. Use the equation to discover how many days a large bag of canis familiaris food will last if it contains 210 cups of food.

(From Unit of measurement 2.2.2)

What Are Non Adjacent Angles,

Source: https://math.libretexts.org/Bookshelves/PreAlgebra/Pre-Algebra_I_(Illustrative_Mathematics_-_Grade_7)/07%3A_Untitled_Chapter_7/7.01%3A_New_Page/7.1.3%3A_Nonadjacent_Angles

Posted by: farmerreanday.blogspot.com